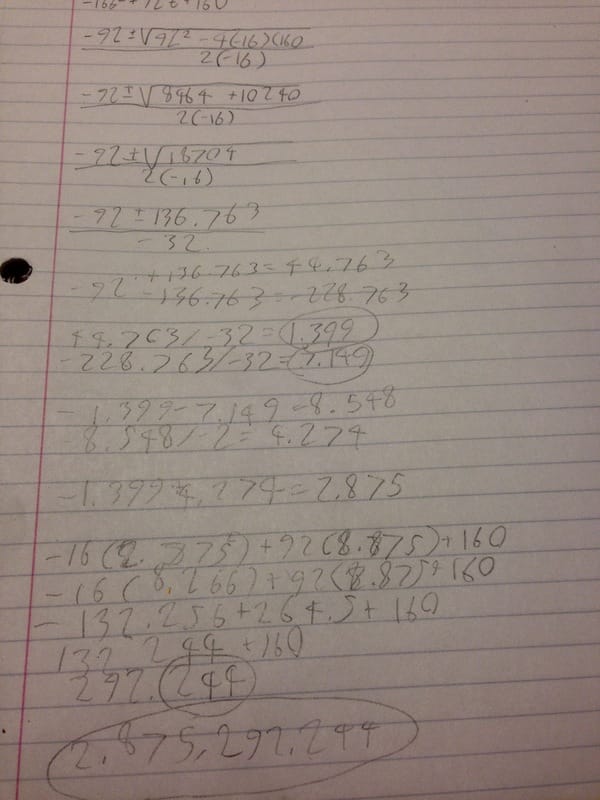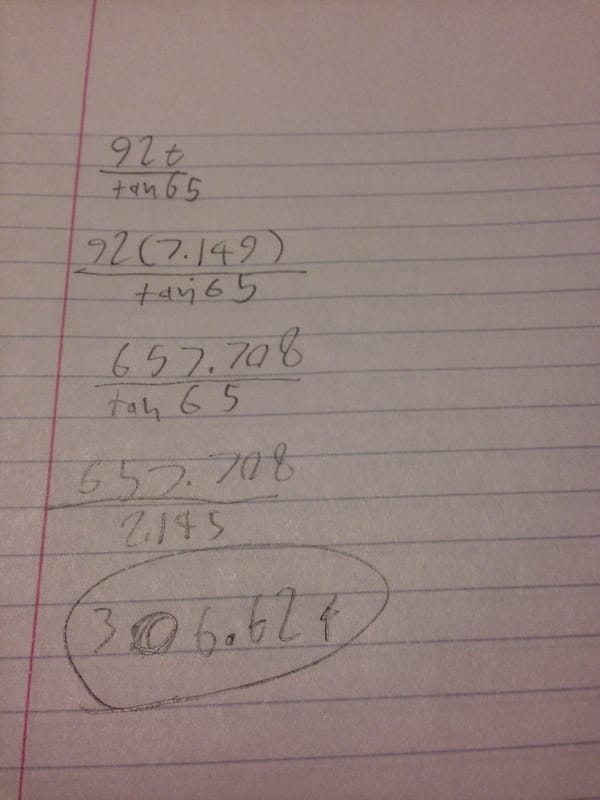Fireworks Problem---Summary
"The Jefferson High junior varsity soccer team has just won the championship. To celebrate this triumph, the school will be putting on a fireworks display. The fireworks will be launched from the top of a school tower. The director isn’t concerned about cost, but he wants your help with the timing mechanism that detonates the fireworks, and he’s also worried about the safety of spectators."
The question is:
-When will the fireworks reach their peak altitude?
-Where will debris from the fireworks touch down?
Before trying to answer these questions, the following information was given:
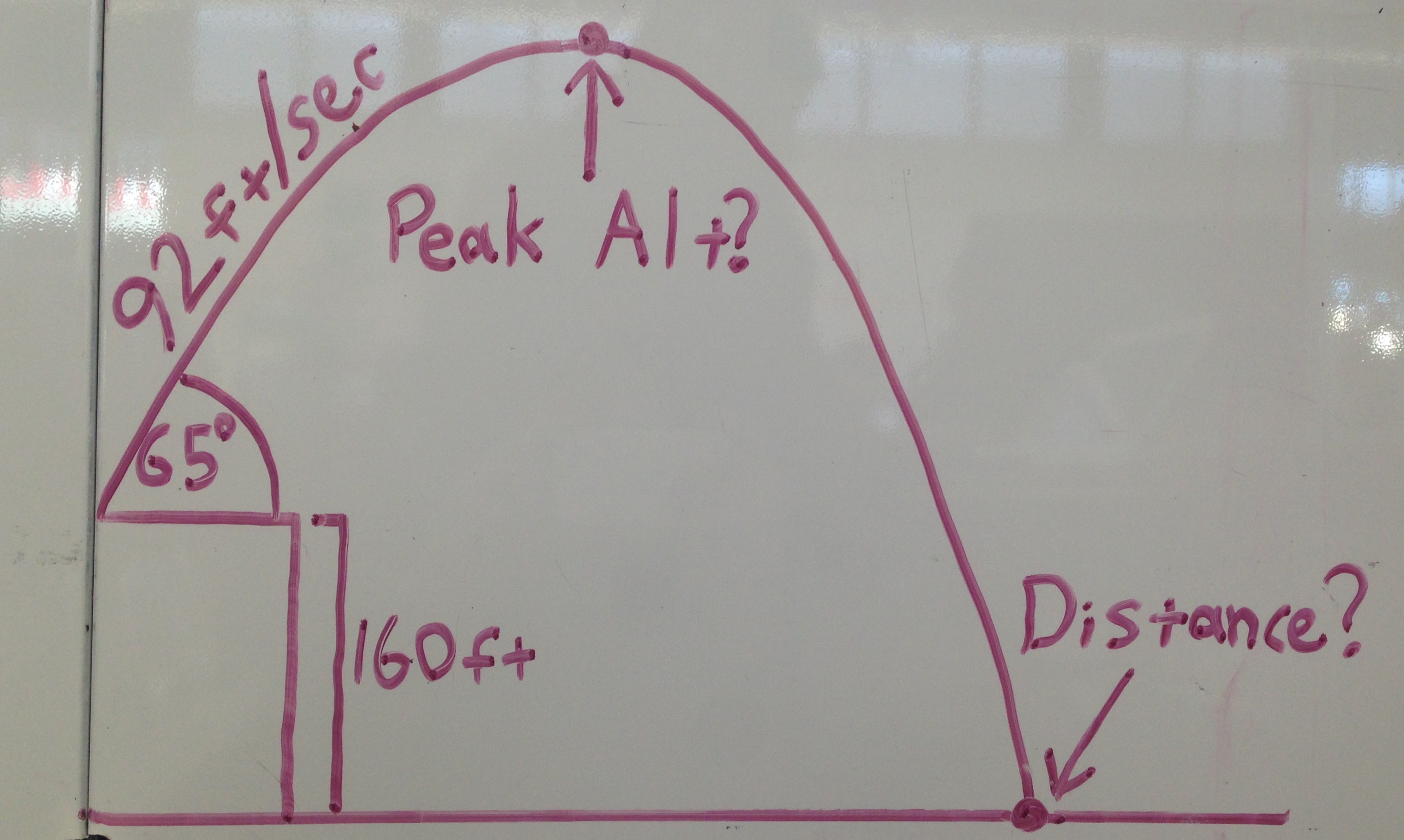
-The fireworks will be launched from a height of 160ft.
-The fireworks will be launched at an upward 65 degree angle.
-The fireworks will have an initial velocity of 92ft/sec.
"The Jefferson High junior varsity soccer team has just won the championship. To celebrate this triumph, the school will be putting on a fireworks display. The fireworks will be launched from the top of a school tower. The director isn’t concerned about cost, but he wants your help with the timing mechanism that detonates the fireworks, and he’s also worried about the safety of spectators."
The question is:
-When will the fireworks reach their peak altitude?
-Where will debris from the fireworks touch down?
Before trying to answer these questions, the following information was given:
-The fireworks will be launched from a height of 160ft.
-The fireworks will be launched at an upward 65 degree angle.
-The fireworks will have an initial velocity of 92ft/sec.
Here is a diagram of the fireworks problem
Fireworks Problem---Process and Solution
Some important questions that I had to begin with were:
-How are the given equations related to the fireworks situation?
-If not the spectators, who else could be in danger of fireworks debris?
-How does the firework detonation timing mechanism work?
Without having the mathematical tools to solve this problem, my first cracks at it were mostly based on my number sense. To find the peak altitude, I picked a time that I thought the firework might reach it's peak altitude, and plugged that value into the first equation. Next, I tried a time value that was higher than the first. If the altitude was higher than the last, I knew that the firework would still be ascending. If the new altitude was lower than the first, I knew that the firework would have started descending, and that it would have reached it's peak altitude at some point in between my first two times. In this way, I continued to deduce the firework's time of peak altitude until I had a solution at least down to the second decimal value. I used a similar "guess and check" method to find the approximate the horozontal distance of the fireworks.
Although it is possible to find the solutions this way, it was incredibly cumbersome. Mr. Carter used the fireworks problem to introduce our quadratics units to us in order to established the connection between mathematical quadratics and it's real world application.
After we had learned all about quadratics, Mr. Carter gave us the formula -16t^2+92t+160, which could help us find the height of the fireworks at any given time. To do this, we had to convert this formula into factored form by plugging it into the quadratic formula.
ax^2+bx+c
Standard form=a^2+b+c
Quadratic formula=-b+/-(square root)b^2-4ac
2a
-16t^2+92t+160
-92+/-(square root of)92^2-4(-16)(160)
2(-16)
-92+/-(square root of)8464+10240
-32
-92+/-(square root of)18704
-32
-92+/-136.763
-32
-92+136.763=44.763
-92-136.763=-228.763
44.763=-1.399=a
-32
-228.763=7.149=b
-32
factored form=(x+a)(x+b)
(x-1.399)(x+7.149)
To find the peak altitude of the fireworks, the x-intercepts must be identified. We converted the original equation into it's factored form because the x-intercepts can be most easily extracted from factored form
(x-1.399)(x+7.149)
x-intercepts: (-1.399,0),(7.149,0)
The next step in finding the peak altitude was to find the midpoint between the two x-intercepts.
(-1.399,0),(7.149,0)
-1.399-7.149
-8.548
-8.548/-2
4.274
-1.399+4.274
Midpoint: 2.875
The midpoint is also the x-coordinate of the parabolas highest point. Now that we had the midpoint, the only thing left to do was plug the midpoint into the original standard form equation.
Midpoint: 2.875
Standard form: -16t^2+92t+160
-16(2.875^2)+92(2.875)+160
-16(8.266)+92(2.875)+160
-132.256+264.5+160
132.244+160
Peak altitude: 292.244
The peak altitude of the fireworks is 292.244 ft
Some important questions that I had to begin with were:
-How are the given equations related to the fireworks situation?
-If not the spectators, who else could be in danger of fireworks debris?
-How does the firework detonation timing mechanism work?
Without having the mathematical tools to solve this problem, my first cracks at it were mostly based on my number sense. To find the peak altitude, I picked a time that I thought the firework might reach it's peak altitude, and plugged that value into the first equation. Next, I tried a time value that was higher than the first. If the altitude was higher than the last, I knew that the firework would still be ascending. If the new altitude was lower than the first, I knew that the firework would have started descending, and that it would have reached it's peak altitude at some point in between my first two times. In this way, I continued to deduce the firework's time of peak altitude until I had a solution at least down to the second decimal value. I used a similar "guess and check" method to find the approximate the horozontal distance of the fireworks.
Although it is possible to find the solutions this way, it was incredibly cumbersome. Mr. Carter used the fireworks problem to introduce our quadratics units to us in order to established the connection between mathematical quadratics and it's real world application.
After we had learned all about quadratics, Mr. Carter gave us the formula -16t^2+92t+160, which could help us find the height of the fireworks at any given time. To do this, we had to convert this formula into factored form by plugging it into the quadratic formula.
ax^2+bx+c
Standard form=a^2+b+c
Quadratic formula=-b+/-(square root)b^2-4ac
2a
-16t^2+92t+160
-92+/-(square root of)92^2-4(-16)(160)
2(-16)
-92+/-(square root of)8464+10240
-32
-92+/-(square root of)18704
-32
-92+/-136.763
-32
-92+136.763=44.763
-92-136.763=-228.763
44.763=-1.399=a
-32
-228.763=7.149=b
-32
factored form=(x+a)(x+b)
(x-1.399)(x+7.149)
To find the peak altitude of the fireworks, the x-intercepts must be identified. We converted the original equation into it's factored form because the x-intercepts can be most easily extracted from factored form
(x-1.399)(x+7.149)
x-intercepts: (-1.399,0),(7.149,0)
The next step in finding the peak altitude was to find the midpoint between the two x-intercepts.
(-1.399,0),(7.149,0)
-1.399-7.149
-8.548
-8.548/-2
4.274
-1.399+4.274
Midpoint: 2.875
The midpoint is also the x-coordinate of the parabolas highest point. Now that we had the midpoint, the only thing left to do was plug the midpoint into the original standard form equation.
Midpoint: 2.875
Standard form: -16t^2+92t+160
-16(2.875^2)+92(2.875)+160
-16(8.266)+92(2.875)+160
-132.256+264.5+160
132.244+160
Peak altitude: 292.244
The peak altitude of the fireworks is 292.244 ft
This is some of the written work that I did in solving for the peak altitude.
Next, we had to determine where debris from the exploded fireworks will land. To do this, we used another equation.
The formula 92t could help us find the horozontal distance of the fireworks given time t.
tan65
The time at which the fireworks touch down is equivelant to the x-intercepts. Since we had already found these, this part was easy. We just needed to plug in both times into the equation for distance.
92t
tan65
92(7.149)
tan65
657.708
tan65
657.708
2.145
306.624
The horizontal distance of the fireworks is 306.624ft. This means that spectators of the fireworks show should be at least 306.624 ft away from the launch site.
The formula 92t could help us find the horozontal distance of the fireworks given time t.
tan65
The time at which the fireworks touch down is equivelant to the x-intercepts. Since we had already found these, this part was easy. We just needed to plug in both times into the equation for distance.
92t
tan65
92(7.149)
tan65
657.708
tan65
657.708
2.145
306.624
The horizontal distance of the fireworks is 306.624ft. This means that spectators of the fireworks show should be at least 306.624 ft away from the launch site.
This is some of the written work that I did in solving for the horizontal distance.
Fireworks Problem---Evaluation
I liked the fireworks problem because it was interesting to learn the connection between mathematical parabolas and the real-life trajectory of the fireworks. I feel that I understood the quadratics unit which is also a reason why I enjoyed doing this problem.
Fireworks Problem---Self Evaluation
The fireworks problem was difficult for me at times. This gave me the opportunity to practice working with my group, which was a good thing because I do not naturally like to collaborate on math problems.
Edits
Sydney
Celebrations: "easy to understand", "clear"
Criticism: "revise solution for distance"
Ana
Celebrations: "clear"
Criticism: "finish problem"
I liked the fireworks problem because it was interesting to learn the connection between mathematical parabolas and the real-life trajectory of the fireworks. I feel that I understood the quadratics unit which is also a reason why I enjoyed doing this problem.
Fireworks Problem---Self Evaluation
The fireworks problem was difficult for me at times. This gave me the opportunity to practice working with my group, which was a good thing because I do not naturally like to collaborate on math problems.
Edits
Sydney
Celebrations: "easy to understand", "clear"
Criticism: "revise solution for distance"
Ana
Celebrations: "clear"
Criticism: "finish problem"