1) Problem Statement
"Mr. Ray is going to buy a new flagpole for the school. However, there are certain regulations regarding how tall the flagpole must be. Mr. Ray needs to find the height of the current flagpole so that he can buy a flagpole that meets the existing requirements." The objective of the "Height of the Flagpole" problem was to find the height of the HTHCV flagpole.
"Mr. Ray is going to buy a new flagpole for the school. However, there are certain regulations regarding how tall the flagpole must be. Mr. Ray needs to find the height of the current flagpole so that he can buy a flagpole that meets the existing requirements." The objective of the "Height of the Flagpole" problem was to find the height of the HTHCV flagpole.
2) Process and Solution
We launched the problem by getting familiarized with the concepts of geometric similarity and scale factors. After this, we visited the flagpole and came up with our own guesses of the height. My initial guess was 25 to 35 feet
In my own words, geometric similarity is when two objects have equal corresponding angles, and proportional corresponding sides.
We launched the problem by getting familiarized with the concepts of geometric similarity and scale factors. After this, we visited the flagpole and came up with our own guesses of the height. My initial guess was 25 to 35 feet
In my own words, geometric similarity is when two objects have equal corresponding angles, and proportional corresponding sides.
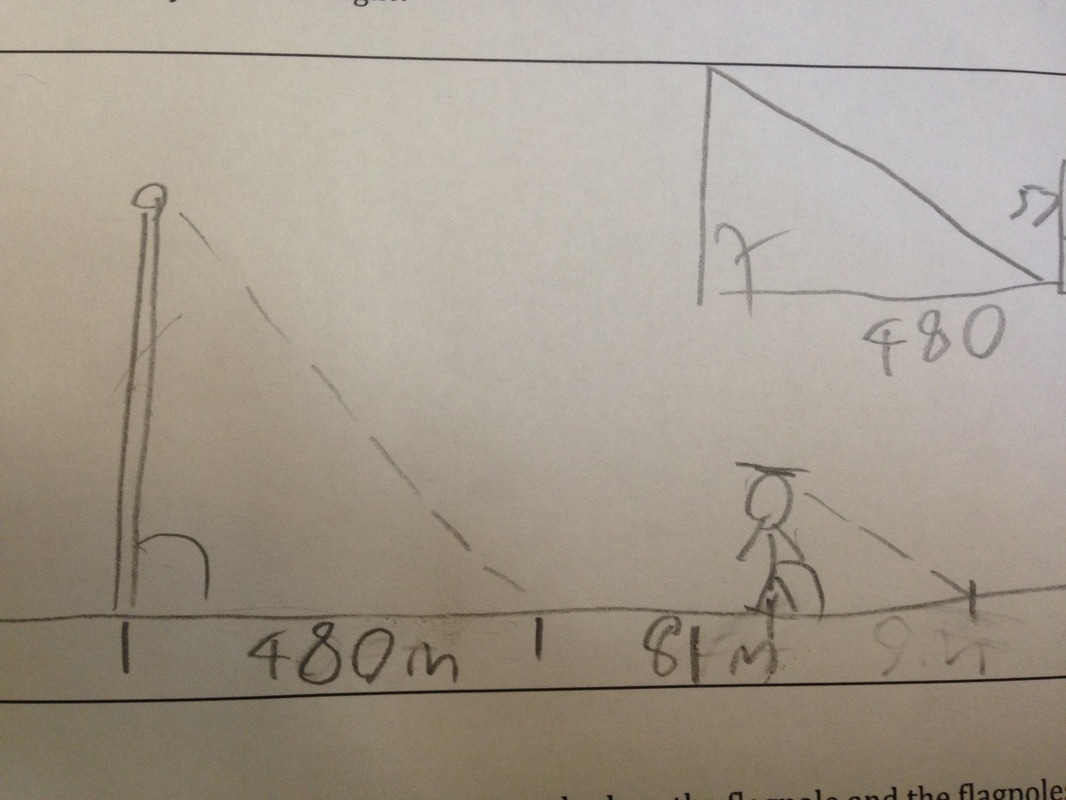
Shadow Method
Below is a diagram representing the principle of the shadow method. The shadow method helped us generate an estimation of the flagpoles height.
Below is a diagram representing the principle of the shadow method. The shadow method helped us generate an estimation of the flagpoles height.
Using the mirror method, we were able to create two similar triangles. We proved similarity using the AA (Angle Angle) theorem. In the diagram above, both triangles have a 90 degree angle between the adjacent and opposite sides. In addition, the triangles share an angle between their adjacent and hypotenuse sides--where the girl’s line of vision reflects off of the mirror. Given these two points, we were able to determine that the mirror method produces two similar triangles.
To estimate the height of the flagpole using the shadow method, we had to measure three things: The height of the person looking down at the mirror; the ground distance between that person and the mirror; the ground distance between the mirror and the base of the flagpole.
Once we had proved similarity and done our measurements, we set-up a proportion equation and cross-multiplied it to solve for x--the height of the flagpole :
2.835.42=15.42x
2.83x=83.58
x=29.53
To estimate the height of the flagpole using the shadow method, we had to measure three things: The height of the person looking down at the mirror; the ground distance between that person and the mirror; the ground distance between the mirror and the base of the flagpole.
Once we had proved similarity and done our measurements, we set-up a proportion equation and cross-multiplied it to solve for x--the height of the flagpole :
2.835.42=15.42x
2.83x=83.58
x=29.53
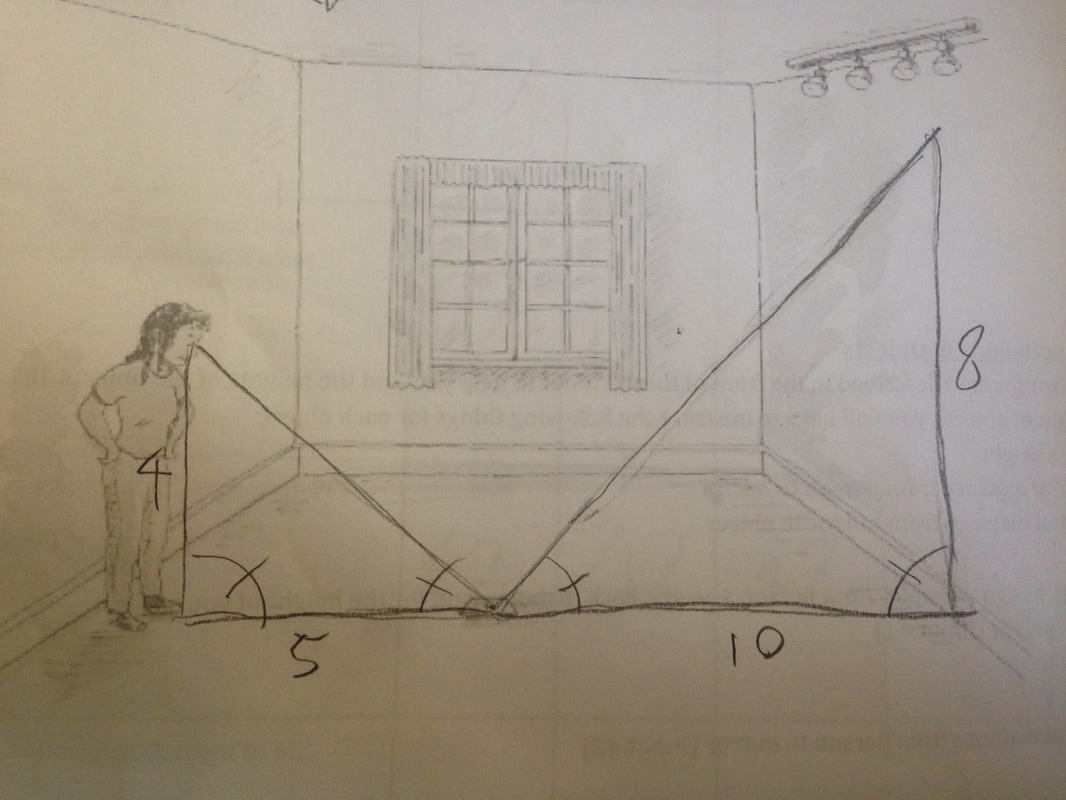
Mirror method
Below is a diagram representing the principle of the mirror method. The mirror method helped us generate an estimation of the flagpoles height.
Below is a diagram representing the principle of the mirror method. The mirror method helped us generate an estimation of the flagpoles height.
Using the mirror method, we were able to create two similar triangles. We proved similarity using the AA (Angle Angle) theorem. In the diagram above, both triangles have a 90 degree angle between the adjacent and opposite sides. In addition, the triangles share an angle between their adjacent and hypotenuse sides--where the girl’s line of vision reflects off of the mirror. Given these two points, we were able to determine that the mirror method produces two similar triangles.
To estimate the height of the flagpole using the shadow method, we had to measure three things: The height of the person looking down at the mirror; the ground distance between that person and the mirror; the ground distance between the mirror and the base of the flagpole.
Once we had proved similarity and done our measurements, we set-up a proportion equation and cross-multiplied it to solve for x--the height of the flagpole :
2.835.42=15.42x
2.83x=83.58
x=29.53
To estimate the height of the flagpole using the shadow method, we had to measure three things: The height of the person looking down at the mirror; the ground distance between that person and the mirror; the ground distance between the mirror and the base of the flagpole.
Once we had proved similarity and done our measurements, we set-up a proportion equation and cross-multiplied it to solve for x--the height of the flagpole :
2.835.42=15.42x
2.83x=83.58
x=29.53
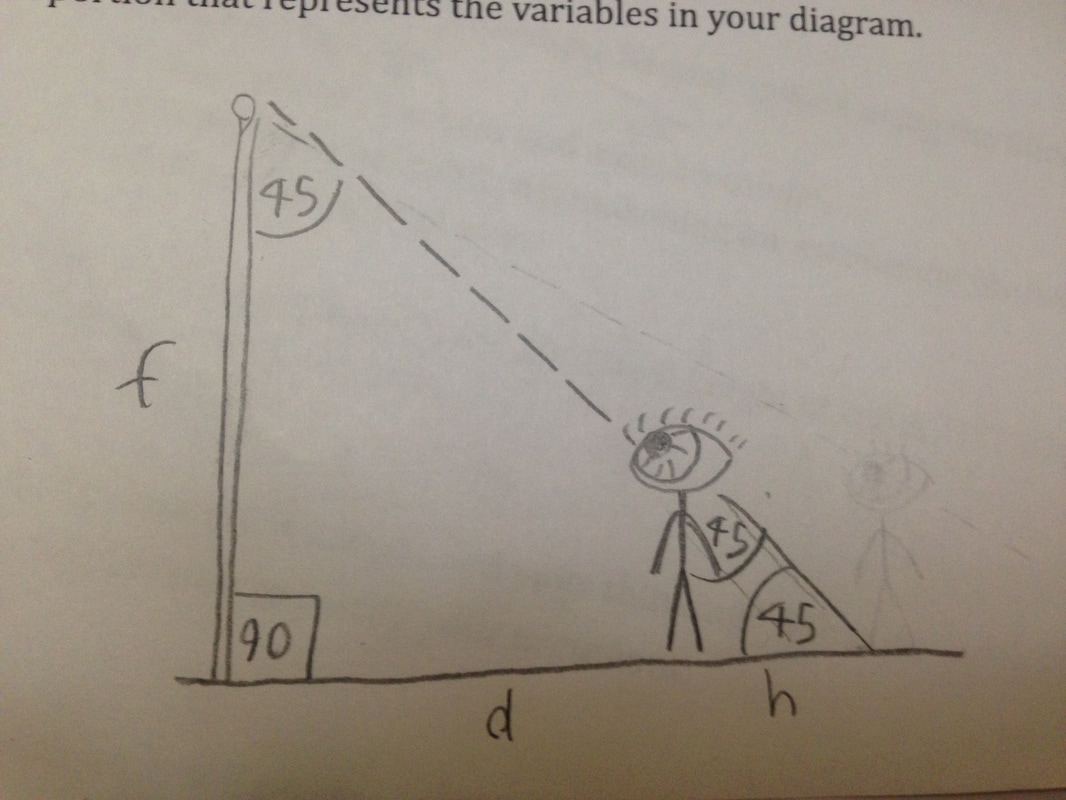
Clinometer Method
Below is a diagram representing the principle of the clinometer method. The clinometer method helped us generate an estimation of the flagpoles height.
Below is a diagram representing the principle of the clinometer method. The clinometer method helped us generate an estimation of the flagpoles height.
Using the clinometer method, we were able to create an isosceles right triangle. In the diagram above, the triangle has a 90 degree angle between its adjacent and opposite sides. In addition, the triangle has a 45 degree angle between its adjacent and hypotenuse sides. Since all triangles must have an angle sum of 180 degrees, we know that the third angle measure must be 45 degrees as well. This symmetry of angles signifies that the triangles arm lengths must be equivalent. Given these points, we determined that the clinometer method produces an isosceles right triangle.
To estimate the height of the flagpole using the clinometer method, we had to measure two things: The height of the person looking down at the mirror; the ground distance between that person and the flagpole. In order for the clinometer method to work, the angle measure of the clinometer when pointed at the flagpole had to be 45 degrees.
Once we had proved similarity and done our measurements, we added the distance between the person and the flagpole and that person’s height. This sum was equal to x--the flagpoles height.
24.17+5.17=29.3
x=29.3ft
To estimate the height of the flagpole using the clinometer method, we had to measure two things: The height of the person looking down at the mirror; the ground distance between that person and the flagpole. In order for the clinometer method to work, the angle measure of the clinometer when pointed at the flagpole had to be 45 degrees.
Once we had proved similarity and done our measurements, we added the distance between the person and the flagpole and that person’s height. This sum was equal to x--the flagpoles height.
24.17+5.17=29.3
x=29.3ft
Best Final Estimation
My best final estimation of the height of the flagpole is 28.77ft. This number is the average of my three previous estimations. I think that averaging my estimates it the most accurate way to define the height of the flagpole because it takes into consideration all methods of solving the problem.
3) Problem Evaluation
I liked this problem because similarity and proofs made sense to me. Also, we got to go outside a lot to take measurements. My favorite part of this project in general was the moments when my group would finally solve a hard problem and it would all start to come together.
4) Self-Evaluation
I would grade myself an A because I did a good job working with my group. When we went outside to take measurements, everyone had a job to do (be the shadow person; measure the shadows; use the clinometer; ect…). Also, some problems in this project had me stumped, so
My best final estimation of the height of the flagpole is 28.77ft. This number is the average of my three previous estimations. I think that averaging my estimates it the most accurate way to define the height of the flagpole because it takes into consideration all methods of solving the problem.
3) Problem Evaluation
I liked this problem because similarity and proofs made sense to me. Also, we got to go outside a lot to take measurements. My favorite part of this project in general was the moments when my group would finally solve a hard problem and it would all start to come together.
4) Self-Evaluation
I would grade myself an A because I did a good job working with my group. When we went outside to take measurements, everyone had a job to do (be the shadow person; measure the shadows; use the clinometer; ect…). Also, some problems in this project had me stumped, so
5) Peer Edits
Peer editor #1: Jackie
Peer editor #1: Jackie
Peer editor #2: Aaron